The whole comprehensive concept of prime numbers is very well considered as the set of the positive integers which are having 2 factors at the maximum. These 2 factors will always be the integer itself and 1. For example, the entire set of factors of a number 6 is 2, 3, 1and 6. In this case, there are 4 factors in total but on the other hand, if people consider the number 7 then the factors will be 1 and 7 which very well clearly states that this particular number is a prime number as it has 2 factors. Hence, 7 can be considered as a prime number and 6 cannot be considered as a prime number rather it is a composite as well as a natural number.
Many people are very much confused about the logics, reasons and formulas to decide if a number is prime or not but actually, there is no such stated formula for finding out the prime number apart from finalizing the respective factors. If a particular number is considered as a prime, then it will have only 2 factor one and that particular number itself. A number that does not follow this particular rule can be considered as the composite number which will very easily mean that it can be easily factored into different kinds of multiple positive integers very well.

The comprehensive historical facts of the prime numbers have been mentioned as follows:
At the very early stage, the prime numbers were founded by Eratosthenes, Greece. This particular person took the example to sieve out the prime numbers from the whole comprehensive list of all the natural numbers in the whole world of numbers and very easily drained out all the entire set of the composite numbers. Students should very efficiently practice this particular method of writing the positive integers from 1 to100 and then they can circle the numbers that fall under the category of being prime and can put out the hyphen to chuck out the composite numbers very easily.
Such numbers possess several kinds of properties and the most important ones are mentioned as follows:
- Each number >1will be easily divided by the prime numbers.
- Each even positive integer that is >2 can be very efficiently defined as the sum of any 2 prime numbers without any kind of issue.
- Apart from the number 2, prime number in the whole number system is considered to be odd. In other words, people can simply say that 2 is the alone number that falls in the category of prime and even.
- 2 given numbers will always be co-prime.
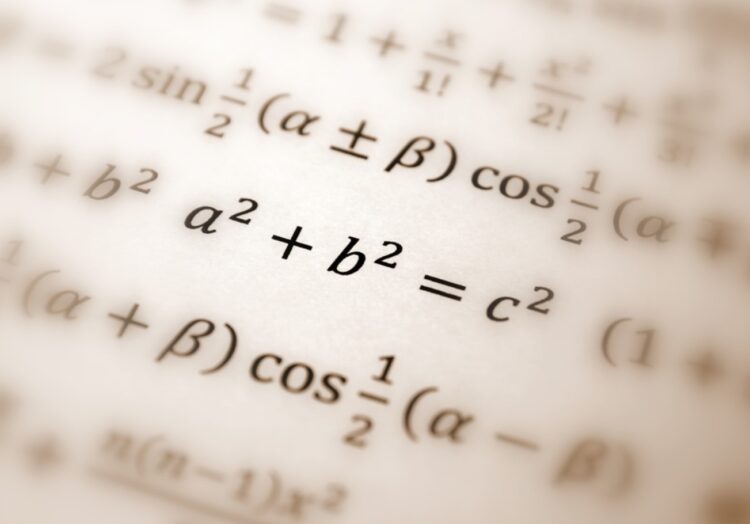
The basic definition of the prime number will very well explain that a particular number will only be having two factors so that it can be efficiently considered as the prime number
2 is termed as the smallest prime in the whole world of numbers and the largest prime number as of January 2024 is 2^ (82,589,933) – 1, This particular number has 2486 2048 digits, and it was discovered under great Internet prime search in the year 2018.
The word integer has been derived from the Latin language which means whole and complete. Hence, it is considered to be a set of whole numbers which include zero, negative and positive numbers in the whole world of number systems. The letter Z very well denotes the integers. The most common examples of integers include -1, -3, 6, 15 and several other numbers.
All the rules of integers are mentioned as follows:
- The total of 2 given positive integers will always be an integer.
- The total of the 2 negative integers will also be an integer.
- The product of two given positive integers will always come out to be an integer.
- The product of two given integers that are negative will always be an integer.
- The total of an integer and respective inverse will always be zero.
- The product of an integer and the reciprocal will always be equal to 1.
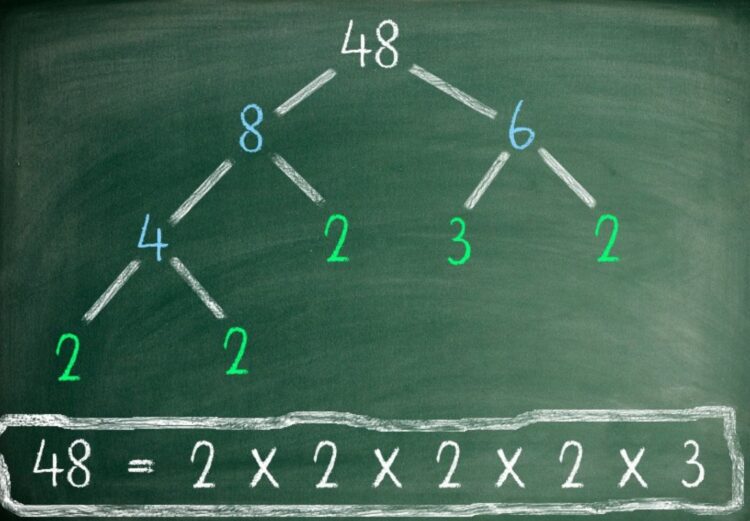
The entire set of properties of the integers has been mentioned as follows:
- Every integer will have the commutative property
- It comes with closure and associative property
- The integers also have distributive property
- It also has the identity-based property
- The integers of additive inverse property
- The integers of multiplicative inverse property
Both the integers as well as prime numbers are considered to be one of the most fundamental concepts in the world of mathematics across the globe for every person associated with this particular field. These kinds of numbers are well-known to build a very strong and robust foundation for the students who are associated with numeric knowledge and want to have great careers in this particular field. Such topics will always allow the students to amplify their academic background and ensure that they are preparing for the right kind of advanced level mathematics in the right direction all the time so that overall purposes are very efficiently achieved and there is no issue for the people in the long run.

Hence, people can very effectively understand it in a very interesting manner with the help of different kinds of organizations for example- Cuemath which is considered to be one of the most important and excellent learning platforms. This particular company utilizes the best of the tools to engage the students with different kinds of concepts and further ensures that people will be learning the best possible things perfectly. The advanced level approaches adopted by this particular company also ensures that there won’t be any kind of issue to the people in the long run. Hence, people can very effectively clear their basics with the help of this particular company because of the best of the methodologies being adopted by the company and the best part is that companies also very well successful in terms of practical applications as well as logical reasoning part of the students so that they can enjoy a lot in the whole process. The company always aims to ensure that everything is very much student-friendly because everything will be based upon logics so that problem-solving skills are very easily encouraged and developed among the students. The approaches adopted by the company are very much flexible as well as brilliant so that mathematical mindsets can be powered, and their dreams can become true very efficiently.











